 Akkor
mondjuk, hogy egy objektum önhasonló, ha véges
számú kicsinyített másával kirakható,
pontosan lefedhetô. Önhasonló egy szakasz, egy négyzet,
egy háromszög vagy egy téglatest; önhasonló,
de nem fraktál. Nem önhasonló ugyanakkor például
egy kör: véges sok kis körbôl nem tudunk nagy kört
csinálni. Ha egy háromszöget a felére kicsinyítünk,
négy kis háromszögbôl pontosan kirakhatjuk az
eredetit; ha a kicsinyítési arány 1/4, ugyanehhez
tizenhat kis háromszögre lesz szükségünk:
a lefedéshez szükséges idomok száma tehát
négyzetesen nô, azaz a kicsinyítési arány
reciprokának második hatványával arányos.
Ha a lefedési kísérletet háromszög helyett
egy szakasszal ismételjük meg, a kis szakaszok száma
csak az elsô hatvány szerint növekszik: harmadakkora
szakaszból három, kilencedakkorából kilenc
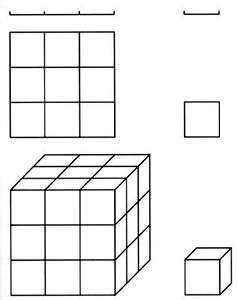
kell. Négyzet lefedésénél a kis idomok száma
a méret négyzetével, kockánál a méret
köbével (azaz harmadik hatványával) szaporodik.
A hatványkitevôben talált számot dimenziónak
is tekinthetjük, és fogalmazhatunk úgy, hogy a szakasz
dimenziója 1, a négyzeté 2, a kockáé
pedig 3, azaz egész számok. Az ábrák
látható idomok tehát önhasonlók, de nem
fraktálok.
Akkor
mondjuk, hogy egy objektum önhasonló, ha véges
számú kicsinyített másával kirakható,
pontosan lefedhetô. Önhasonló egy szakasz, egy négyzet,
egy háromszög vagy egy téglatest; önhasonló,
de nem fraktál. Nem önhasonló ugyanakkor például
egy kör: véges sok kis körbôl nem tudunk nagy kört
csinálni. Ha egy háromszöget a felére kicsinyítünk,
négy kis háromszögbôl pontosan kirakhatjuk az
eredetit; ha a kicsinyítési arány 1/4, ugyanehhez
tizenhat kis háromszögre lesz szükségünk:
a lefedéshez szükséges idomok száma tehát
négyzetesen nô, azaz a kicsinyítési arány
reciprokának második hatványával arányos.
Ha a lefedési kísérletet háromszög helyett
egy szakasszal ismételjük meg, a kis szakaszok száma
csak az elsô hatvány szerint növekszik: harmadakkora
szakaszból három, kilencedakkorából kilenc
kell. Négyzet lefedésénél a kis idomok száma
a méret négyzetével, kockánál a méret
köbével (azaz harmadik hatványával) szaporodik.
A hatványkitevôben talált számot dimenziónak
is tekinthetjük, és fogalmazhatunk úgy, hogy a szakasz
dimenziója 1, a négyzeté 2, a kockáé
pedig 3, azaz egész számok. Az ábrák
látható idomok tehát önhasonlók, de nem
fraktálok.